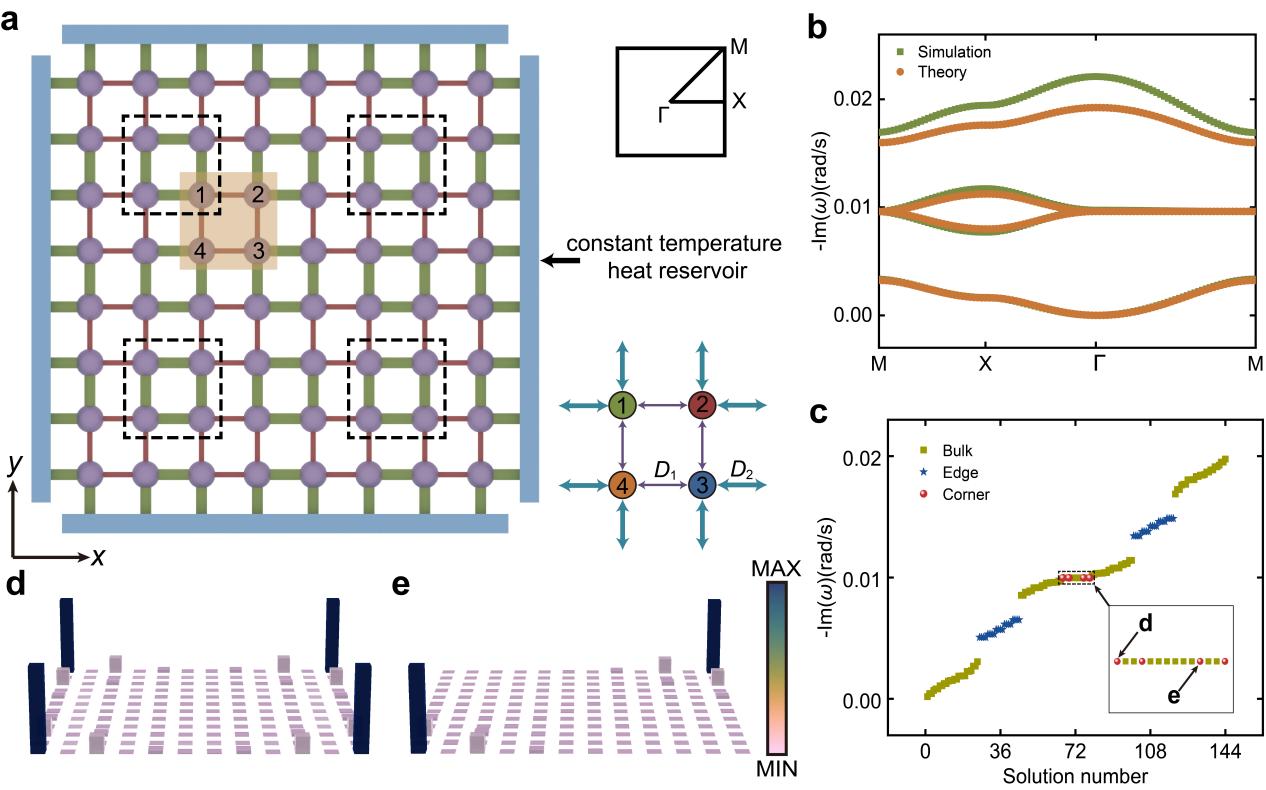
近日🤵🏿♀️🍦,杏悦/应用表面物理国家重点实验室黄吉平教授课题组与浙江大学信息与电子工程学院李鹰教授课题组合作,在纯热扩散系统中实现了高阶拓扑绝缘体,同时其角态嵌在体态之内而不是位于能隙之内,该角态有助于高效散热和局域化热管理。相关成果以“Higher-Order Topological In-Bulk Corner State in Pure Diffusion Systems”为题发表于《Physical Review Letters》🏒。我系黄吉平教授与浙江大学李鹰教授为论文的共同通讯作者,我系博士生刘周费同学与浙江大学博士后曹培超博士为论文的共同第一作者🙅🏽♀️🫅,合作者还包括中国工程物理研究院研究生院须留钧研究员🚼、新加坡国立大学许国强博士。该工作是在陶瑞宝院士的启发与鼓励下完成的。 在过去的几十年里🦹🏿♀️,超越朗道对称性破缺范式的拓扑材料,引起了凝聚态物理学界的极大兴趣。其中🐲,高阶拓扑绝缘体是一种新型的拓扑材料🌗,其独有的角态超越了传统的体边对应原理。除了真实的材料系统之外,高阶拓扑绝缘体已经在很多经典波系统中得到了实现,例如光子学🤹🏿♀️、声学、力学等。最近几年,以热学为代表的扩散系统已经成为了一个实现拓扑物理的崭新平台✊🏽,由于其支配方程与波动系统的相比,本质上截然不同,因此研究扩散系统的拓扑物理会出现很多新奇现象。目前已经有相关工作报道了高阶拓扑绝缘体在热学系统中的实现,但是这些工作实现的角态均位于能隙之中👌,而另外一种嵌在体内的高阶拓扑角态(在光学中被认为是一种连续谱中的束缚态)还没有被实现🧑🏭。 本工作利用球棒结构,并且通过施加固定边界条件,实现了扩散版本的二维Su-Schrieffer-Heeger模型(图1)🚒。在凝聚态物理中🚣🏻,该模型是一种具有偶极矩的高阶拓扑绝缘体。由于该模型满足C4v对称性和手征对称性,因此其角态是嵌在体内的。本工作从理论🧑🦲、模拟🚵🏿♂️😶、实验三个方面来研究该嵌在体内角态的热学行为🐁。对于非平庸的拓扑角态,角球的温度演化较快且遵循指数衰减🙍♂️,同时其温度场呈现局域分布⛴,角球的温度场对相邻球的温度场影响很小。另外🕖,本工作也比较了体内角态和能隙中角态的不同热学行为。相对于后者🚽,前者周围温度场对角球温度场的影响较小。因此,该角态在高效散热和局域化热管理方面具有应用前景。 论文地址:https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.132.176302 图1🔏😜:扩散二维Su-Schrieffer-Heeger模型中的体内角态。